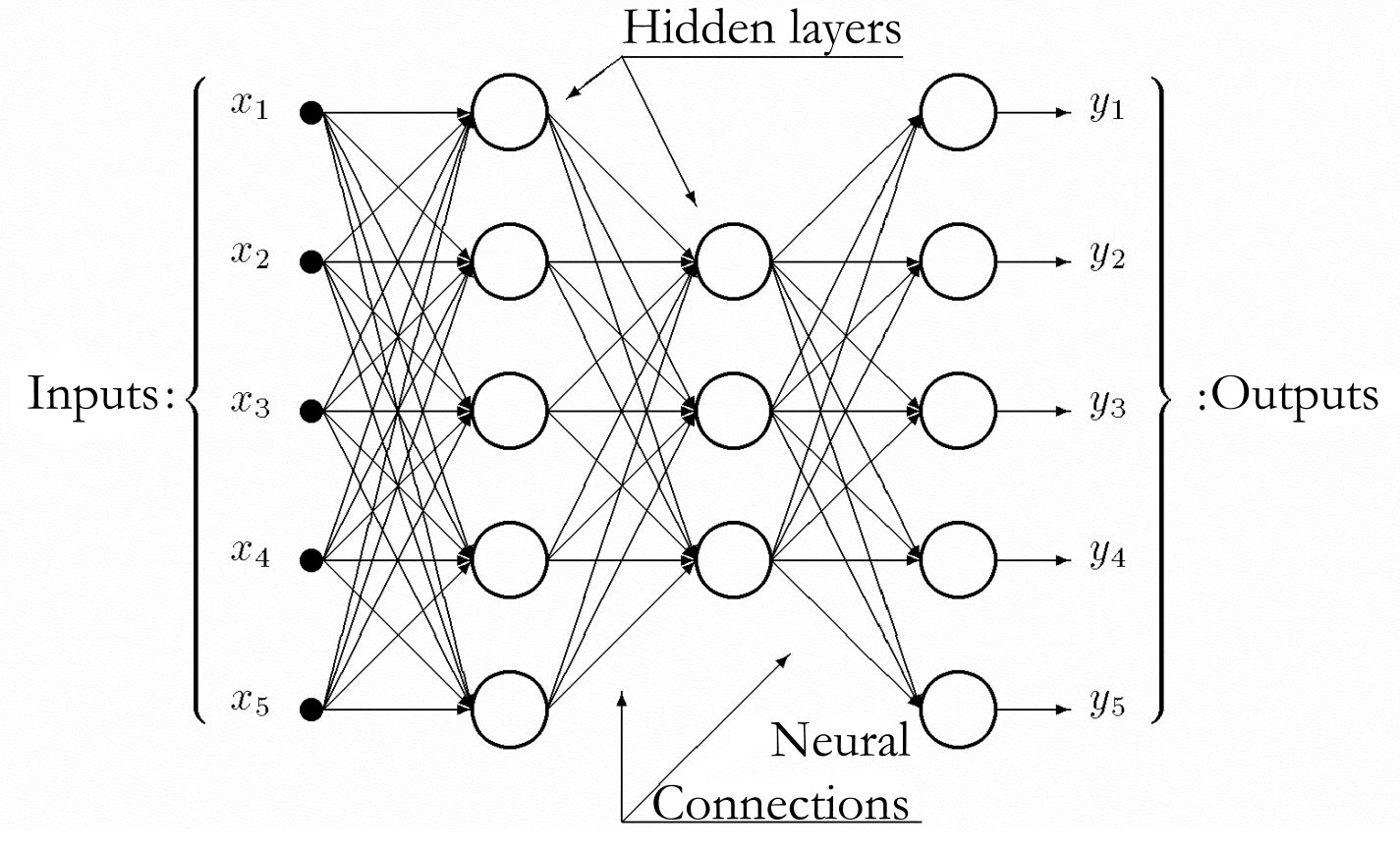
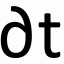I am only covering feedforward neural networks in this project. General features of such networks are:
- Neurons are grouped into one input layer, one or more hidden layers and an output layer.
- Neurons are not connecting to each other within the same layer.
- Each neuron of a hidden layer connects to all the neurons of the previous and the next layer.
- The directions of connections between two layers are homogenous, directed from the inputs towards the outputs.
A neural network meeting the requirements above is called a general feedforward network:
Graph of a general feedforward neural network
Let’s assume we have a network with M layers. Each layer contains Nl neurons, where l=1,…,M. The first layer contain N0=n inputs. In this layer each neuron obtains the same X(x0,1;x0,2;…;x0,m) input vector. The output layer contain NM=m neurons. The net input of the i. neuron of layer l. is xl,I , and it is computed as below:
\[x_{l,i}=\sum\limits_{j=1}^{N_{l-1}} w_{l,i,j}y_{l-1,j}+b_{l,i,j},\ \ \text{where} \ \ i=1,…N_l , l=1,…M.\]
Where wl,i,j is the weight between the j. neuron of layer l-1. and the i. neuron of layer l. and bl,i,0 is the bias value of the neuron. The values of yl-1,j are obtained through the neuron of the previous layer. The output of the i. neuron of the l. layer after the activation:
\[y_{l,i}=f\left(x_{j,i}\right)=\frac{1}{1+e^{-cx_{l,i}}},\ \ c>0.\]
The training pattern and the error function
Let us imagine a neural network with n inputs, m outputs and with any number of hidden layers. Let there be given a pattern set {(x1, t1), …, (xp, tp)} of p number of elements, each of which consisting of n and m dimensional vector pairs, normalized within the same interval as the value set of the activation function. All the primitive functions of the neurons in the network are supposed to be continuous and differentiable.
When the xi input vector of the pattern set is fed to the network as input the result will be an output vector yi, which of course differs from the target vector ti. While training the neural network the aim is to get the output vector as close to the target vector as possible. To measure this distance we define an error (or also called objective loss) function E. A popular choice for E is the sum-squared error:
\[E_{i}=\frac{1}{2}\sum\limits_{i=1}^{p} \left| y_i – t_i \right|^2.\]
While training E is to be minimized in the function of the weights. Having minimized the error for the vector i we step towards the vector i+1, and the network is expected to interpolate between the patterns.
The error function of sigmoid in case of one single neuron
E is an m dimensional function of the weights. This function is a surface which has a global minimum point but it may also have local minimum points.
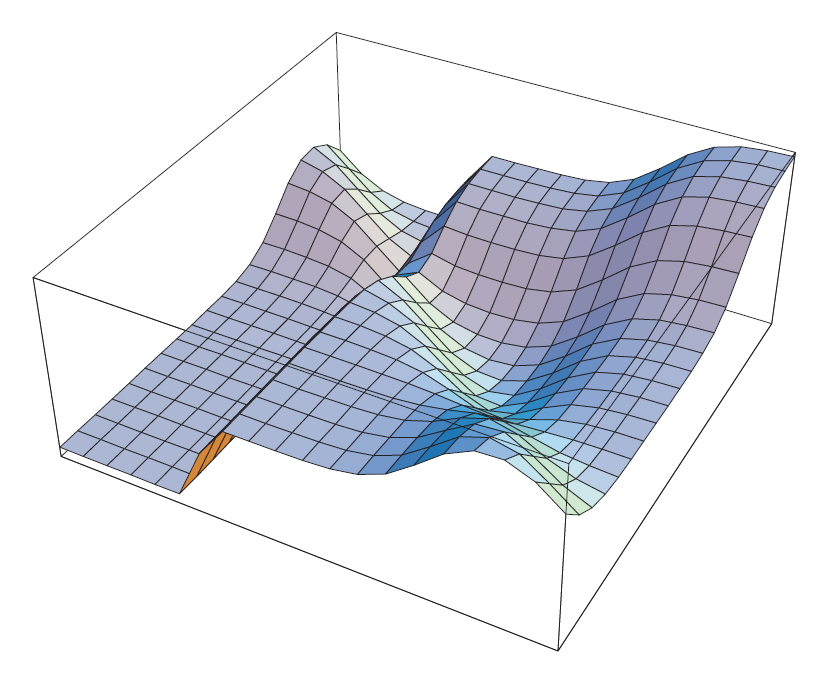 A local minimum of a complex error function
A local minimum of a complex error function