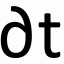If there are multiple layers in a neural network the inner layers have neither target values nor errors. This problem remained unsolved until the 1970s when mathematicians found the backpropagation algorithm to be usable for this particular problem.
Backpropagation provides a way to train neural networks with any number of hidden layers. The neurons don’t even have to be organized into layers, the algorithm will work fine with any directed (inputs to outputs) graph of neurons that don’t contain cycles. These networks are called feedforward networks or directed acyclic graphs.
First we have to define a so called Error function that represents the difference between the outputs and the target values. Let’s make the error function compute the
\[\frac{1}{2}\left(y_i-t_i\right)^2.\]
values.
The error function only depends on the activation functions, so it can be described as the continous and differentiable function of w1, w2, … wl weights of a network containing l number of weights:
\[\nabla E=\left( \frac{\partial E}{\partial w_1}, \frac{\partial E}{\partial w_2}, …, \frac{\partial E}{\partial w_l} \right).\]
Input vectors are fed to the network through the input layer. While the vector k is fed, the neurons of the first layer compute their outputs, and propagate them forward to the next layer. The output of the network is the output of the last layer. The error of the last layer can easily be computed knowing the output vector:
\[E=\min\limits_{W}\sum\limits_{k=1}^{p} E^k=\min\limits_{W} \frac{1}{2} \sum\limits_{k=1}^{p} \sum\limits_{i=1}^{n} \left( y_{M,i}^k-t_{i}^k\right)^2.\]
The partial derivative of the error function by the weights of neurons in the output layer:
\[\frac{\partial E}{\partial w_{M,i,j}}=\sum\limits_{k=1}^{p}\frac{\partial E^k}{\partial y_{M,i}}\cdot\frac{dy_{M,i}^k}{dx_{M,i}}\cdot\frac{\partial x_{M,i}^k}{\partial w_{M,i,j}}=\]
\[\sum\limits_{k=1}^p\left(y_{M,i}^k-t_i^k\right)\frac{dy_{M,i}^k}{dx_{M,i}}y_{M-1,j}^k.\frac{dy_{l,j}^k}{dx_{l,j}}=f’\left(x_{l,j}^k\right)\]
Introducing the value of δkM,i as below:
\[\delta_{M,i}^k=\left(y_{M,i}^k-t_i^k\right)f’\left(x_{M,i}^k\right),\ \ \text{where}\ \ i=1,… ,N_M\]
The partial derivative of the error function for the output layer:
\[\frac{\partial E}{\partial w_{M,i,j}}=\sum\limits_{k=1}^p\delta_{M,i}^k y_{M-1,j}^k\]
Any neuron at a hidden layer l. affects only the layer l+1. directly so it affects the output layer indirectly.
\[\frac{\partial E^k}{\partial y_{l,j}}=\sum\limits_{j=1}^{N_{l+1}}\frac{\partial E^k}{\partial y_{l+1,j}}\cdot\frac{dy_{l+1,j}}{dx_{l+1,j}}\cdot\frac{dx_{l+1,j}}{dy_{l,i}}=\sum\limits_{j=1}^{N_{l+1}}\frac{\partial E^k}{\partial y_{l+1,j}}\cdot\frac{dy_{l+1,j}}{dx_{l+1,j}}.w_{l+1,j,i}\]
The value of δkM,i can be generalized for all layers:
\[\delta_{l,i}^k=f’\left(x_{j,i}^k\right)\sum\limits_{j=1}^{N_{l+1}}\delta_{l+1,j}^k w_{l+1,j,i},\ \ \text{where}\ \ i=1,…,N_l;l=M-1,…,l.\]
According to the last equation the errors of the layer l+1. propagate back to the previous layer. The partial derivative of the error function depending from any of the layers can be expressed as:
\[\frac{\partial E}{\partial w_{M,i,j}}=\sum\limits_{k=1}^p \delta_{M,i}^k y_{M-1,j}^k.\]
The last step is to modify the weights in the direction which decreases the error. This direction is the inverse of the direction of the partial derivative of the last equation:
\[w_{l,i,j}^{(t+1)}=w_{l,i,j}^{(t)}-\alpha_t\frac{\partial E^{(t)}}{\partial w_{l,i,j}}.\]
The value of αt is a constant and it is called learn rate. The above update must be applied repeatedly. The error will have to converge to 0 if the learn rate αt is chosen as:
\[\sum\limits_{t=1}^{\infty}\alpha_t=+\infty,\ \ \text{and} \ \sum\limits_{t=0}^{\infty}\alpha_t^2<\infty.\]
The above method is called offline or batch version of the backpropagation algorithm because the weights are only updated after processing all of the input patterns.