Dear Reader,
I have been through a very productive weekend, I have managed to implement a simple matrix partitioning algorithm, and also a matrix multiplier function that multiplies 4×4 matrices using SSE intrinsics.
Partitioning is not yet as efficient as I know it could be, because it creates 4×4 blocks no matter what. Even in the case of a 3×1 matrix, it will become a 4×4 block, and the SSE multiplier function will process all the unnecessary values too. Even worse, in the case of an 5×1 vector it would create two 4×4 blocks, one block containing only one scalar value. So there is still a lot of space for improvement.
At first the performance suffered very heavily because of the way I created the matrix partitions. Every time a matrix multiplication was necessary, I re-created all the necessary partitions in memory. The result was that the speed of the calculations dropped to approximately half of what I was able to achieve with a highly optimised but naively implemented multiplier (the previous record speed measurement values were 151MCpS on 8 hardware threads, and 459MCpS on 40 hardware threads).
Then I have introduced a new way of storing the partitions. Basically I have moved the partition storage to class level, and made sure that the partitions were never deleted. The values contained in the partitions still need to be updated every time a multiplication happens and memory is allocated for them as the partitions are added, but they never get deleted – well at least not until the matrix itself is deleted. Instead they are being reused. This leads to a situation that when a matrix is used both in transposed and non-transposed modes, the partitions will occupy the maximum dimension both horizontally and vertically. For example, in the case of a 12*2 matrix, the non-transposed partitions will occupy [3×1] x [4×4] cells, and the transposed partitions will occupy [1×3]x[4×4] cells, making the total memory usage to [3×3] x [4×4].
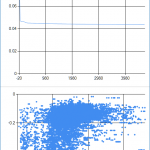
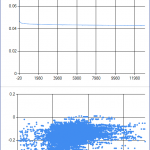
The results speak for themselves:
On a 4GHz Core i7 with 8 hardware threads the speed of the calculations reached 195MCpS (on the left), and on a 3GHz dual Xeon with 40 hardware threads it reached 615MCpS (on the right). This is 6093 kCpS/GHz/core for the core i7 machine, and 5125 kCpS/GHz/core for the dual Xeon machine.
And as I have written above I still have ideas for further optimisations.
I was playing with the thought of storing only pointers in the partitioned blocks instead of values, but in the end I didn’t implement this. This approach would require much more attention to detail and a complete redesign as it is very dangerous. The biggest problem with this is that I would need to make sure that every 4 length row in a partitioned block is continuous in memory, because this is a requirement for the _mm_loadu_pd SSE function that loads a vector of doubles. However, I can’t guarantee that this will happen with the current design that stores both transposed and non-transposed matrices in the same continuous vector in memory.
In the meantime I have installed the NVidia CUDA SDK, and to my pleasant surprise its sample applications already contain a matrix-multiplication algorithm. I guess this will have to wait at least until the next weekend.
In case you’ve missed my previous posts the updated source code can be found here:
https://github.com/bulyaki/NNTrainerLib