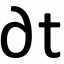Preconditioning weights
The outcome and speed of a learning process is influenced by the initial state of the network. However, it is impossible to tell which condition will be the most ideal. The commonly accepted way is initializing weights by uniformly distributed random numbers on the (0,1) interval.
Preconditioning data
Very often the training set fed to the network consists of real-time measurement data measured in various units and quantities. These numbers must be normalized before using them to train the network. The normalizing interval depends on the activation function of the network: in case of the sigmoid it should be (0,1) and in case of the hyperbolic tangent it should be (-1,1).
Avoiding local minima
Gradient descent algorithms attempt to move towards the global minimum of the error function. If the error surface does not have local minima the situation is very simple because any step downwards will take us closer to the global minimum point. However, error surfaces of real problems can be very complex. If there are local minimum points in the error surface the gradient descent algorithm can get trapped in one of them.

One way of escaping local minima can be by starting the training process with the online algorithm as it produces enough noise to make the algorithm escape from local minima. Once the network has reached the global minimum it is worth switching to the batch method so that the global minimum is determined at a greater accuracy.

The momentum
A very commonly used extension to the backpropagation algorithm is the use of a so-called momentum term which means that the weights are modified with the weighed sum of the actual and all the previous gradients. Altering the weights will look like this:
\[\Delta w_{l,i,j}^{(t+1)}=-\alpha(1-\beta)\frac{\partial E^{(t)}}{w_{l,i,j}}+\beta\Delta w_{l,i,j}^{(t)}=-\alpha(1-\beta)\sum\limits_{k=0}^t \beta^k\frac{\partial E^{(t-k)}}{\partial w_{l,i,j}}.\]
When the gradients following each other are equal the exponentially weighed sum increases causing larger changes in the weights. When the following gradients change sign this sum decreases. In practice the momentum term is to be set in the interval (0,1).